The modulo operator, denoted by %, is a fundamental mathematical operation in JavaScript. This deceptively simple-looking operator is crucial in various applications, from basic everyday coding to advanced problem-solving and dynamic animations.

In this guide, we’ll investigate how the modulo operator works and we’ll explore several real-life applications.

Understanding the modulo operator

When we divide one number (the dividend) by another number (the divisor), we get a quotient. But, often, the divisor does not go in evenly. In those cases, the number that is left over after the division operation is complete is referred to as the remainder. For example, when we divide 10 by three, we get a quotient of three and a remainder of one. We can also write this as 1 (mod 3).

In JavaScript, the modulo operator gets the remainder of a division operation. It takes two numbers, the dividend and the divisor, and returns the remainder after division. The syntax for using it is as follows:

10 % 3; // 1

//We can also use the modulo operator on floating-point numbers. For example:
10.5 % 3; // 1.5
10.5 % 3.5; // 0

This may seem like a simple operation, but it has many applications that are far more complex than getting the remainder of a division operation. Let’s explore some of these applications.

Modulo operator applications

In everyday coding, the modulo operator serves a variety of essential purposes. Let’s take a look at some typical and practical use cases.

Checking for even or odd numbers

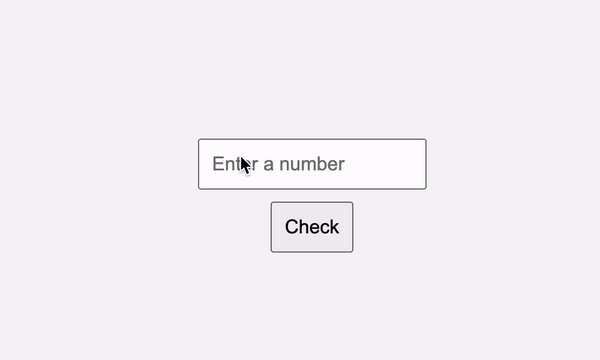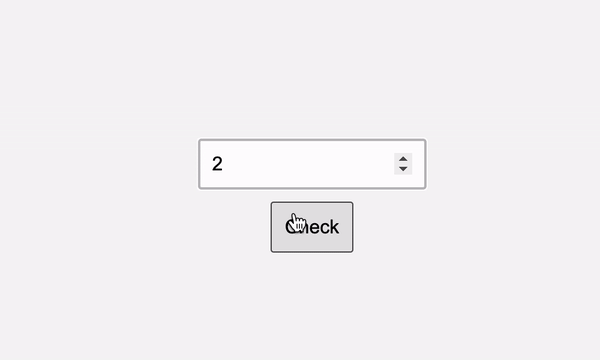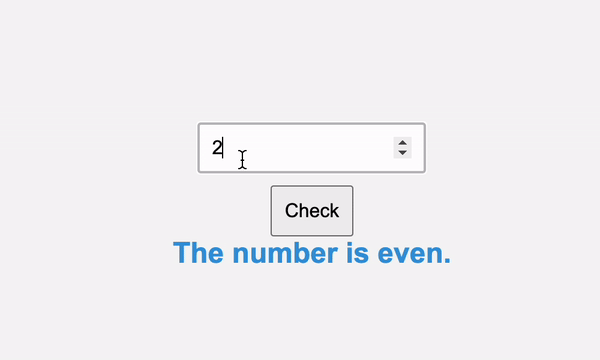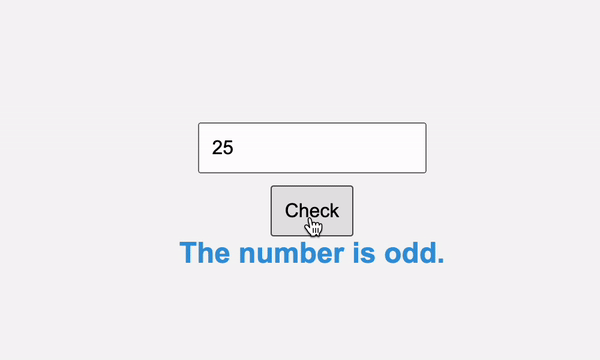
We can determine whether a number is even or odd by checking if it’s divisible by two, like so:

function isEvenOrOdd(num) {
  if (num % 2 === 0) {
    return "even";
  } else {
    return "odd";
  }
}
// Check if 7 is even or odd
console.log(isEvenOrOdd(7));
// Result: odd

Here’s the even and odd checker in action:

The modulo operator is valuable when we need to categorize numbers or perform different actions based on their parity. For example, when designing a spreadsheet application, we may want to alternate the row background colors to improve readability. Using the modulo operator, we can quickly achieve this by applying different colors to even and odd rows.

Verifying divisibility

We can determine if one number is evenly divisible by another, which has applications in checking factors and multiples:

function isDivisible(dividend, divisor) {
  return dividend % divisor === 0;
}

The modulo operator helps check if a given number is a multiple of another. This has several real-life applications, such as setting up scheduling to ensure tasks occur at regular intervals or arranging elements in a grid or matrix to maintain a structured layout:

Setting up scheduling tasks

In the below code, we check scheduling to determine when to water the garden:

// Function to check if it's time to water the garden
function isTimeToWater(currentTime, wateringInterval) {
  if (currentTime % wateringInterval === 0) {
    return true; // It's time to water the garden.
  } else {
    return false; // It's not time to water the garden.
  }
}
// Simulated time in minutes
const currentTime = 120; // 2 hours (in minutes)
// Define the watering interval (in minutes)
const wateringInterval = 30; // Water every 30 minutes
if (isTimeToWater(currentTime, wateringInterval)) {
  console.log(`It's time to water the garden.`);
} else {
  console.log(`It's not time to water the garden yet.`);
}
// Result: It's time to water the garden.

In this scenario, it’s time to water the garden when dividing the current time by the watering interval yields no remainder (i.e., it’s evenly divisible), ensuring the task occurs at precise intervals:

See the Pen
Garden Watering Reminder using Modulo Operator by Timonwa (@timonwa)on CodePen.

Arranging elements in a grid

Here we check to determine if a given number of elements can be arranged in a grid of a specified size:

// Function to arrange elements in a grid
function arrangeInGrid(elements, rows, cols) {
  if (elements % (rows * cols) === 0) {
    return `Elements can be arranged in a ${rows}x${cols} grid.`;
  } else {
    return `Elements cannot be perfectly arranged in a ${rows}x${cols} grid.`;
  }
}
// Check if 30 elements can be arranged in a 5x6 grid
const elements = 30;
const rows = 5;
const cols = 6;
console.log(arrangeInGrid(elements, rows, cols));
// Result: Elements can be arranged in a 5x6 grid.

In this example, there’s no remainder when the number of elements is divided by the product of the number of rows and columns Therefore, the elements can be perfectly arranged in the grid, ensuring a structured layout.

Implementing cyclic sequences

We can use the modulo operator to create cyclic patterns, such as cycling through an array, iterating through a sequence of states, or implementing infinite loops. Creating cyclic patterns or sequences is a fundamental application of this arithmetic operation.

Cycling through an array

In the below code, we iterate through the dates of the week:

const daysOfWeek = [
  "Monday",
  "Tuesday",
  "Wednesday",
  "Thursday",
  "Friday",
  "Saturday",
  "Sunday",
];
// Function to cycle through the days of the week
function cycleDays(index) {
  return daysOfWeek[index % daysOfWeek.length];
}
// Let's cycle through the days:
for (let i = 0; i < 10; i++) {
  console.log(`Day ${i + 1}: ${cycleDays(i)}`);
}
// Result:
// Day 1: Monday
// Day 2: Tuesday
// Day 3: Wednesday
// Day 4: Thursday
// Day 5: Friday
// Day 6: Saturday
// Day 7: Sunday
// Day 8: Monday
// Day 9: Tuesday
// Day 10: Wednesday

Here, the cycleDays function uses the modulo operator to ensure that we loop back to the beginning of the week once we reach Sunday.

Generating patterns

We can create patterns, such as repetitions of numbers or characters, using the modulo operator to control the sequence:

function generatePattern(length) {
  const pattern = [];
  for (let i = 0; i < length; i++) {
    pattern.push(i % 3);
  }
  return pattern;
}
// Generate a pattern of length 10
console.log(generatePattern(10));
// Result: [0, 1, 2, 0, 1, 2, 0, 1, 2, 0]

We can use the modulo operator to develop dynamic content or designs with structured patterns or sequences. For example, we can generate a pattern of circles for the dynamic background for a website and use the modulo operator to apply different colors to odd and even rows of the pattern.

Precise animation

The modulo operator is a valuable tool for creating animations with precision and synchronization. Let’s explore two essential aspects of animation:

Looping animations

Looping animations are commonly used for creating elements that continuously cycle through a sequence. Here, the modulo operator ensures the animation loops seamlessly. Let’s take a look at a simple example:

// Function to create a looping animation frame
function createLoopingFrame(frameCount, duration) {
  const interval = duration / frameCount;
  let currentFrame = 0;
  setInterval(() => {
    const frame = currentFrame % frameCount;
    console.log(`Displaying frame ${frame}`);
    currentFrame++;
  }, interval);
}
// Create a 3-frame looping animation with a 2-second duration
createLoopingFrame(3, 2000);
// Result:
// Displaying frame 0
// Displaying frame 1
// Displaying frame 2
// Displaying frame 0
// { ... Runs forever ... }

In this example, the createLoopingFrame function uses the modulo operator to ensure the animation loops through frames. This concept is widely applied in creating elements like rotating loading spinners and seamlessly repeating background animations. It is a continuous loop of animation that never ends:

See the Pen
Bouncing Balls Loop Animation by Timonwa (@timonwa)on CodePen.

Synchronized animations

Synchronization is crucial when multiple elements or animations need to run simultaneously or in harmony. The modulo operator is useful for handling this synchronization.

For example, in a web application, data is often loaded in stages. Each stage may display a spinner, leading to an unpleasant “jumping” effect when a new spinner replaces the previous one. This issue occurs because the CSS animation restarts with each new spinner.

We can address this issue with a technique that uses the CSS animation-delay property. By setting negative animation-delay values when a spinner mounts, we synchronize the animations. This approach ensures smooth transitions between spinners during data loading, providing a better user experience:

@keyframes spinAnimation {

  to {

    transform: rotate(360deg);

  }

}

.spinner {

  animation: 1000ms infinite spinAnimation;

  animation-delay: var(--spinner-delay);

}

const Spinner = (props) => {

  const mountTime = React.useRef(Date.now() % 1000);

  return <Spinner style={{ "--spinner-delay": `-${mountTime.current}ms` }} />;

};

In this example, the Spinner component uses the modulo operator to synchronize its animations. The mountDelay variable calculates the time remaining until the next second, which sets the animation-delayvalue. This ensures that the animation starts simultaneously for all spinners, preventing a “jumping” effect.

Date and time calculations

Date and time calculations often involve using the modulo operator for various purposes, such as finding the day of the week for a given date. Here’s an example showing how to calculate the day of the week using the modulo operator within Zeller’s congruence algorithm:

function getDayOfWeek(year, month, day) {
  if (month < 3) {
    month += 12;
    year -= 1;
  }
  const K = year % 100;
  const J = Math.floor(year / 100);
  const dayOfWeek =
    (day +
      Math.floor((13 * (month + 1)) / 5) +
      K +
      Math.floor(K / 4) +
      Math.floor(J / 4) -
      2 * J) %
    7;
  const days = [
    "Saturday",
    "Sunday",
    "Monday",
    "Tuesday",
    "Wednesday",
    "Thursday",
    "Friday",
  ];
  return days[(dayOfWeek + 7) % 7];
}
const year = 2023;
const month = 7; // July
const day = 18;
const dayOfWeek = getDayOfWeek(year, month, day);
console.log(`The day of the week for ${year}-${month}-${day} is ${dayOfWeek}.`);
// Result: The day of the week for 2023-7-18 is Tuesday.

Complex computational problems

Modular arithmetic plays a fundamental role in problem solving across various domains. At its core, modular arithmetic deals with the remainder of integer division. It operates within a fixed range and wraps around when the maximum value is reached. This modular wrapping property makes it a powerful tool for solving complex problems.

A 12-hour clock is a classic application of modular arithmetic. If it’s currently 10:00 a.m., we can intuitively determine the time after adding a certain number of hours. This is done by taking the remainder when dividing by 12. For example, the time will be 3:00 p.m. If we add five hours. This is because 10 + 5 = 15, and15 % 12 = 3:

const currentHour = 10; // Current hour
const hoursToAdd = 5; // Hours to add
// Calculate future hour
const futureHour = (currentHour + hoursToAdd) % 12;
console.log(
  `When it's ${currentHour}:00, the time will be ${futureHour}:00 after ${hoursToAdd} hours.`
);
// Result: When it's 10:00, the time will be 3:00 after 5 hours.

There are several scenarios where modular arithmetic is crucial:

• • Cryptography and information security: Key for encryption algorithms, including the widely-used RSA algorithm. The difficulty of factoring large semiprime numbers relies on modular arithmetic properties
  • Data structures and algorithms: Used  in various data structures like circular buffers and data transformations. Algorithms that involve cyclical patterns or cyclical data structures often utilize modular arithmetic for optimized computation
  • Computer graphics: Employed for pixel operations, creating patterns, and handling screen boundaries. It helps ensure seamless transitions between screen edges and enables efficient image manipulation
  • Error detection and correction: Employed in error-detection codes and error-correction algorithms. These ensure the accurate transmission of data, especially in network communication and data storage
  • Game development: Used to create periodic behaviors like character movement, object animation, and handling game levels. It’s essential for defining game mechanics and interactions

Handling screen boundaries in games

In a 2D game, modular arithmetic helps keep a character within the screen boundaries by keeping the character’s position (X, Y) within the screen’s width and height:

// Ensure the character stays within screen boundaries
function updateCharacterPosition(
  characterX,
  characterY,
  screenWidth,
  screenHeight
) {
  characterX = (characterX + screenWidth) % screenWidth; // Wrap X position
  characterY = (characterY + screenHeight) % screenHeight; // Wrap Y position
  return { characterX, characterY };
}
// Simulate character movement within screen boundaries
console.log(updateCharacterPosition(2, 5, 10, 10));
// Result: { characterX: 2, characterY: 5 }
// Simulate character movement beyond screen boundaries
console.log(updateCharacterPosition(12, 5, 10, 10));
// Result: { characterX: 2, characterY: 5 }

Here, the updateCharacterPosition function ensures that a character’s position remains within the specified screen boundaries. It uses the modulo operator to wrap the character’s X and Y positions.

If the character’s position exceeds the screen width or height, the modulo operation effectively “wraps” the character back to the opposite side of the screen, keeping it within bounds. This is particularly useful for scenarios where characters or objects must navigate seamlessly within a confined screen area, as demonstrated by the function’s output.

Conclusion

The modulo operator is a simple yet incredible tool in JavaScript. It goes beyond basic remainders, finding applications in numerous coding scenarios. Whether you’re checking for even or odd numbers, ensuring divisibility, creating cyclic patterns, synchronizing animations, or advanced problem-solving, the modulo operator is a powerful tool to have in your arsenal.

By understanding the modulo operator and its applications, you can improve your coding skills and become a better developer. I encourage you to experiment with the modulo operator’s capabilities and explore its potential. You’ll be amazed at what you can achieve with this simple yet powerful operator.